Talk:Hexagonal tiling

Optical illusion

The yellow hexagons don't look regular in this image, though I know it's just an optical illusion. Double sharp (talk) 15:42, 8 August 2009 (UTC)[reply]

You can think of the hexagons as truncated equilateral triangles, since that's what they are in this coloring. Tom Ruen (talk) 00:53, 9 August 2009 (UTC)[reply]

Here's a chart of some of the different tessellations related to this one. I based it off of this table.

Construction of Archimedean Tessellations in Euclidean Space with Hexagonal Symmetry
Starting tessellation Operation	Symbol {p,q}	Hexagonal tiling {6,3}	Triangular tiling {3,6}
Truncation (t)	t{p,q}	Truncated hexagonal tiling	Truncated triangular tiling
Rectification (r) Ambo (a)	r{p,q}	Trihexagonal tiling
Bitruncation (2t) Dual kis (dk)	2t{p,q}	Truncated triangular tiling	Truncated hexagonal tiling
Birectification (2r) Dual (d)	2r{p,q}	Triangular tiling	Hexagonal tiling
cantellation (rr) Expansion (e)	rr{p,q}	Rhombitrihexagonal tiling
Snub rectified (sr) Snub (s)	sr{p,q}	Snub trihexagonal tiling
Cantitruncation (tr) Bevel (b)	tr{p,q}	Truncated trihexagonal tiling

However, it might be more helpful to see it as simply another column in a table of tilings. After all, the other columns can simply be thought of as spherical tilings, and the columns to the right as hyperbolic tilings.

Construction of Archimedean Solids and Tessellations
Symmetry		Tetrahedral	Octahedral		Icosahedral
Starting solid Operation	Symbol {p,q}	Tetrahedron {3,3}	Cube {4,3}	Octahedron {3,4}	Dodecahedron {5,3}	Icosahedron {3,5}	Hexagonal tiling {6,3}	Triangular tiling {3,6}	Heptagonal tiling {7,3}	Order-7 triangular tiling {3,7}
Truncation (t)	t{p,q}	truncated tetrahedron	truncated cube	truncated octahedron	truncated dodecahedron	truncated icosahedron	Truncated hexagonal tiling	Truncated triangular tiling	Truncated heptagonal tiling	Truncated order-7 triangular tiling
Rectification (r) Ambo (a)	r{p,q}	tetratetrahedron	cuboctahedron		icosidodecahedron		Trihexagonal tiling		Triheptagonal tiling
Bitruncation (2t) Dual kis (dk)	2t{p,q}	truncated tetrahedron	truncated octahedron	truncated cube	truncated icosahedron	truncated dodecahedron	truncated triangular tiling	truncated hexagonal tiling	Truncated order-7 triangular tiling	Truncated heptagonal tiling
Birectification (2r) Dual (d)	2r{p,q}	tetrahedron	octahedron	cube	icosahedron	dodecahedron	triangular tiling	hexagonal tiling	Order-7 triangular tiling	Heptagonal tiling
cantellation (rr) Expansion (e)	rr{p,q}	rhombitetratetrahedron	rhombicuboctahedron		rhombicosidodecahedron		rhombitrihexagonal tiling		Rhombitriheptagonal tiling
Snub rectified (sr) Snub (s)	sr{p,q}	snub tetratetrahedron	snub cuboctahedron		snub icosidodecahedron		snub trihexagonal tiling		Snub triheptagonal tiling
Cantitruncation (tr) Bevel (b)	tr{p,q}	truncated tetratetrahedron	truncated cuboctahedron		truncated icosidodecahedron		truncated trihexagonal tiling		Truncated triheptagonal tiling

As you can see, the truncation of {3, n} for any natural number n always has two hexagons and one n-gon meeting at each vertex, and the dual of {3, n} always has three n-gons meeting at each vertex. When n=6, the truncation is two hexagons plus one hexagon (three hexagons), and the dual is three hexagons, so the truncation and dual of {3, 6} are the same as each other; each has three hexagons meeting at a vertex.2601:2C1:C001:1F20:80B9:A1B0:4862:7768 (talk) 23:36, 16 July 2017 (UTC)[reply]

Hexagonal tiling is rigid?

The article says that the hexagonal tiling is "rigid" unlike the square tiling, which can be deformed into parallelograms. It seems to me that the hexagons could be flattened while keeping the edges the same length and connected in the same fashion. Pciszek (talk) 04:58, 5 September 2011 (UTC)[reply]

Agreed, like brick pattern

is a flattened hexagonal tiling, still equal-edge lengths. SockPuppetForTomruen (talk) 23:58, 5 September 2011 (UTC)[reply]

3 types of monohedral convex hexagonal tilings

(This discussion has been moved from WP:RD/Mathematics#Hexagonal tiling.)

The Guardian writes[1] that "It was proved in 1963 that there are exactly three types of convex hexagon that tile the plane.", but our article treats "hexagonal tiling" as a synonym to the honeycomb. What are the other two? Or is that quote a misunderstanding, and the proof was actually about the colorings? — Sebastian 18:49, 20 August 2015 (UTC)[reply]

There might be something in Tilings and Patterns. I do get confused about what it means to have types. Some isohedral variations are here Hexagonal_tiling#Topologically_equivalent_tilings, taken from tilings and Patterns (list of 107 isohedral tilings, p.473-481). Tom Ruen (talk) 19:00, 20 August 2015 (UTC)[reply]

This webpage shows the three:[2]. The constraints look like they imply a symmetry. Tom Ruen (talk) 19:07, 20 August 2015 (UTC)[reply]

Reinhardt showed that there are only three types of convex hexagons which tessellate:

Type 1: B+C+D=A+E+F=360°, a=d (p2, 2222 symmetry?) lattice has 2 tiles

Type 2, A+B+D=C+E+F=360°, a=d, c=e (pgg, 22× symmetry?) lattice has 4 tiles

Type 3, A=C=E=120°, a=a', c=c', e=e' (p3, 333 symmetry?) lattice has 3 tiles

Thank you, that answers my question. It seems they are all isohedral, although type 2 involves mirroring. If one colored that, it would give a wavy pattern. (I can do that with the SVG file, but unfortunately I can't post it here for copyright reasons.) I can imagine these might also have some practical relevance as the resonances of a graphite lattice. — Sebastian 19:49, 20 August 2015 (UTC)[reply]

Interestingly, none of them are constrained as parallelogons, but these have single tile lattices. By symmetry, I'd guess these would be a special case of type 1 when all opposite edges are equal. Tom Ruen (talk) 20:05, 20 August 2015 (UTC)[reply]

(edit conflict) Right, but type 1 could be called a semi- or more exactly, a

2+1 \over 6

-parallelogon, since 2 pairs of sides are parallel, and one has the same length. Type 2 looks like a||d, but that's just they way they did the picture. As for the special case, yes, that would be the p2 (2222) picture in our article, or, further degenerated, the stretched hexagon. — Sebastian 20:22, 20 August 2015 (UTC)[reply]

Here's a best quick guess, taking hexagonal 1-isohedral tilings from http://www.jaapsch.net/tilings/, but there are actually 6 cases listed there. Tom Ruen (talk) 20:53, 20 August 2015 (UTC)[reply]

3 types of monohedral convex hexagonal tilings
1	2	3
p2, 2222	pgg, 22×	p3, 333

b=e B+C+D=360°	b=e, d=f B+C+E=360°	a=f, b=c, d=e B=D=F=120°
2-tile lattice	4-tile lattice	3-tile lattice

Thank you for the great reply; this far exceeds what I had hoped for. This would be a great addition to the article; I am tempted to add it to the beginning. But there is one problem: The article is currently laid out for one specific tiling, the one based on the regular hexagon. If we change this article to cover all hexagonal tilings, some parts of the article will need adjustment, and it will not be possible to adjust the sidebar. Maybe I shouldn't worry about that, seeing that the articles Hexagon and Pentagon also mostly cover the regular case, and their sidebar also is only dedicated to that case. Another point to consider is that we already have a big overlap between this article and Hexagonal lattice, which might open the option of merging that article with the regular hexagonal tiling. However, I don't think there's a precedence for that, and I don't know what such an article should be called; I just wanted to mention it now, so we can brain storm on the best solution. — Sebastian 23:16, 20 August 2015 (UTC)[reply]

I think it belongs here, same topology, lower symmetry to the regular form, but I've not seen any original sources for it. Tom Ruen (talk) 00:00, 22 August 2015 (UTC)[reply]

By "[no] original sources", I understand you mean that you're afraid your source from euler.slu.edu is not original. But there's no need to to refer to original sources; sources need to be reliable, and I don't think there's reason to assume that Saint Louis University is not reliable for this case. We can just write "Reinhardt (1918), cited in SLU ...". (Of course you're using a different order for the naming, but it's mathematically the same; I checked it.) BTW, I just looked at the other source you cite, http://www.jaapsch.net/tilings/, and I don't see where you see six cases. — Sebastian 00:59, 22 August 2015 (UTC)[reply]

I'm glad you checked. I used the Java Application at www.jaapsch.net. In it, there are 6 hexagonal/convex/isohedral cases listed. It looks like they are regrouped from 13 isohedral cases Named (P6-1&8&10&12&13 (pg); P6-2&9 (pg); p6-3&7 (p2); p6-4 (pgg); p6-5 (pgg); p6-6&11 (p3)) Tom Ruen (talk) 01:21, 22 August 2015 (UTC)[reply]

You mean the tiling viewer at http://www.jaapsch.net/tilings/tilingapp.htm? That just says "A plugin is needed to display this content", which is very unhelpful, since it gives no hint which plugin. But the many new tilings at http://www.jaapsch.net/tilings, such as "k-Isohedral tilings, k>3", give me a clue what the confusion is about: There are just 3 different tiles, but you can arrange them differently to get more than 3 different tilings. I now realize that I didn't have to limit my question at Talk:Pentagonal tiling#Roses and other distinct tilings from special cases just to special cases. — Sebastian 01:46, 22 August 2015 (UTC)[reply]

Yes, it's Java. I had to run the Java outside my browser because of security stupidity. Here's the 13 isohedral tilings, from Tilings and Patterns. p.481. Some of them are already in the article. (OOPS, I called it isogonal, should say isohedral!!) Tom Ruen (talk) 02:13, 22 August 2015 (UTC)[reply]

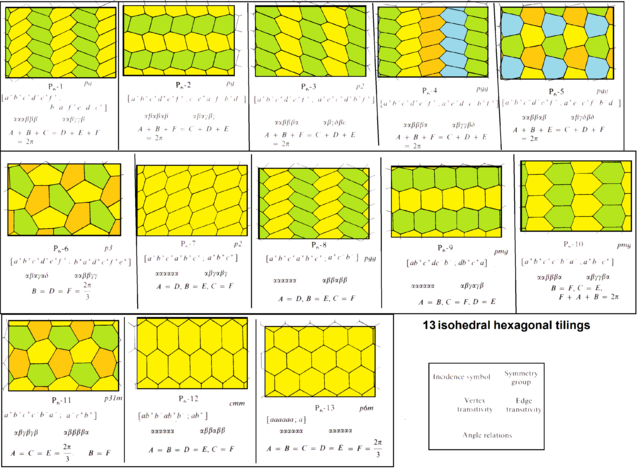
Terminology

I think we have a serious terminology problem. When we speak of n tilings or n types of tilings, do we mean

(as the article seems to assume) n different sets of conditions for the sides and angles of the underlying tile, or
(as we seem to be using it in this section) n different symmetries. (Where we are only looking at monohedral arrangements.)? — Sebastian 02:56, 22 August 2015 (UTC)[reply]

I completed the images of the 13-isohedral tilings as defined in Tilings and Patterns. I'm not sure how charactize this list besides isoehedral. I'm not sure what to call the list of 3 except "3 types of convex monohedral hexagonal tilings" or whatever the sources say. Tom Ruen (talk) 03:40, 22 August 2015 (UTC)[reply]

Is it error?

Uniform colorings

In table two rows Wythoff in first column, but first linked with Schläfli symbol, second - with Wythoff symbol. Jumpow (talk) 13:37, 25 March 2017 (UTC)[reply]

Fixed. Thanks! Tom Ruen (talk) 02:05, 26 March 2017 (UTC)[reply]

External links modified

Hello fellow Wikipedians,

I have just modified one external link on Hexagonal tiling. Please take a moment to review my edit. If you have any questions, or need the bot to ignore the links, or the page altogether, please visit this simple FaQ for additional information. I made the following changes:

Added archive https://web.archive.org/web/20100919143320/https://akpeters.com/product.asp?ProdCode=2205 to http://www.akpeters.com/product.asp?ProdCode=2205

When you have finished reviewing my changes, you may follow the instructions on the template below to fix any issues with the URLs.

This message was posted before February 2018. After February 2018, "External links modified" talk page sections are no longer generated or monitored by InternetArchiveBot. No special action is required regarding these talk page notices, other than regular verification using the archive tool instructions below. Editors have permission to delete these "External links modified" talk page sections if they want to de-clutter talk pages, but see the RfC before doing mass systematic removals. This message is updated dynamically through the template {{source check}} (last update: 5 June 2024).

If you have discovered URLs which were erroneously considered dead by the bot, you can report them with this tool.
If you found an error with any archives or the URLs themselves, you can fix them with this tool.

Cheers.—InternetArchiveBot (Report bug) 09:09, 3 November 2017 (UTC)[reply]

Add height-to-width ratio?

I was in need of this measurement for the purpose of making a tiled surface, but could find no good reference for how much to offset every line from the previous one. I made some calculations at https://www.omnicalculator.com/math/hexagon and added the height-to-width ratio to the Hexagon page (under Parameters) for others to use. Perhaps this should go into Hexagonal tiling? JanGB (talk) 07:23, 11 July 2019 (UTC)[reply]

Monohedral convex hexagonal tilings

Under Monohedral convex hexagonal tilings "type 2", there are images of two tilings that are apparently identical apart from the colouring. Is this correct? It looks to me as if the left-hand all-yellow version is just a miscolouring of the right-hand one (according to the convention that I believe is intended, that green tiles should be the mirror image of yellow). Or is there any valid explanation? Tai Ling (talk) 21:03, 22 February 2024 (UTC)[reply]

Types of monohedral "tiling"

It says under "Monohedral convex hexagonal tilings" that "There are 3 types of monohedral convex hexagonal tilings". This seems untrue for any feasible method of counting "tilings", as I would understand it. I assume what is actually meant is that there are three different convex tile types (as defined in the table) that are capable of tiling the plane monohedrally? Tai Ling (talk) 22:03, 22 February 2024 (UTC)[reply]